Purpose
Outcomes in Randomized Controlled Trials (RCT) are often computed as changes from baseline of finite scales (e.g., pain assessments going from 0 to 10). When subjects receive effective treatment over time they may reach the limit of a finite scale. In that case, the score limitation at the bottom of the finite scale, called “floor effect”, can cause a saturation of the observed outcome. This can lead to underestimation of the treatment effect measured using the difference between an active and a control group in an RCT.
This abstract discusses how saturation should be accounted for, while designing the sample size and the inclusion criteria in an RCT. First, it assesses the impact of the saturation of the outcome on the study power. Secondly, it shows how to compute the expected proportion of subjects with a saturated outcome, the saturation rate (SR), when designing a study. Lastly, it discusses how to adapt the study design to reduce the SR and/or its impact.
Methods
The power of a study is generally computed by considering the efficacy measurement (EM) assessed at the end of treatment (EOT) as two Gaussians, one for the active group and the other for the placebo group. Nevertheless, when the ideal Gaussians are distributed beyond the scale limitation, saturation happens and the real saturated distributions are no longer exact Gaussians. Accounting for this transformation, the drop of the effective study power, caused by the saturation, is estimated. Two other parameters can influence this effective power: the sample size N of the study and the ratio K = SDBaseline/SDResponse (SD: Standard Deviation), illustrating whether the variability of the EM at EOT comes from the baseline or from the response.
To assess the SR that could occur in a RCT, the “true” mean and SD of the EM at EOT are assumed to be known. The expected SR in the active group can then be computed as a function of the standardized mean M* defined as the ratio between the mean and the SD.
Finally, the use of a minimum required baseline score as an inclusion criterion is assessed
using several simulations, in order to reduce the SR and the resulting power loss. Furthemore, the inflation of the sample size, needed to compensate the loss in power, was assessed for several examples.
Results
Figure 1 shows that the effective power drops with a high SR. Starting from a power of 80%, the power drops to approximately 65% for K = 0.5, 50% for K = 1, and 35% for K = 1.5, as the SR grows from 0% to 50%. For a similar SR, larger values of K induces lower power. In other words, if the differenece of EM at EOT is more caused by the difference between the subjects at baseline than from their difference in response (K >1), the power drops faster. This figure presents the evolution for N = 100, but the drop in power was similar for other sample sizes.
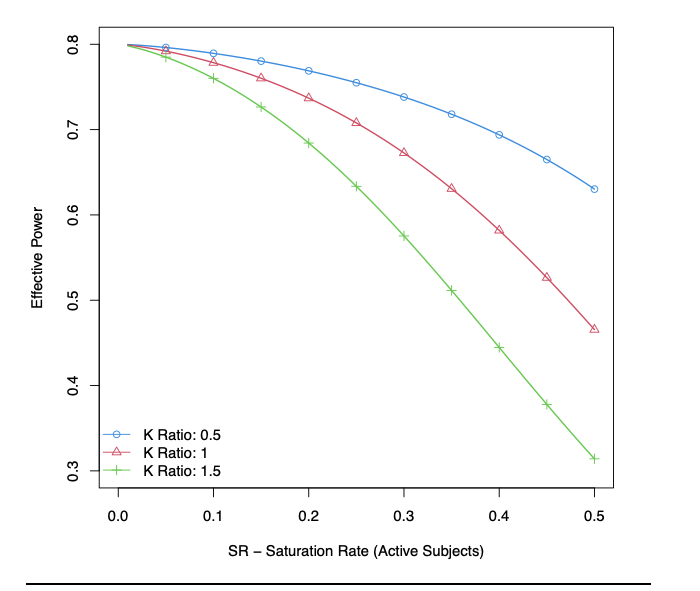
Figure 1:Effective Power in function of the Saturation Rate of active subjects for different K, the ratio between the SD at baseline and the SD of the change from baseline (SD: Standard Deviation), considering a sample size N = 100.
Figure 2 presents the expected SR as a function of the standardized mean M*: the higher the M*, the lower the SR. Combining the results of Figures 1 and 2, we have, as examples:
- An M* of 0.5 generates an SR of 31% inducing a relative loss of power up to 30%. An increase of the sample size up to 80% would be necessary to compensate such high loss.
- An M* of 1 generates an SR of 16%, inducing a relative loss of power below 10% and requiring a sample size increase of 5-20%.
- An M* of 2 generates an SR of 2% with a power close to the targeted one.
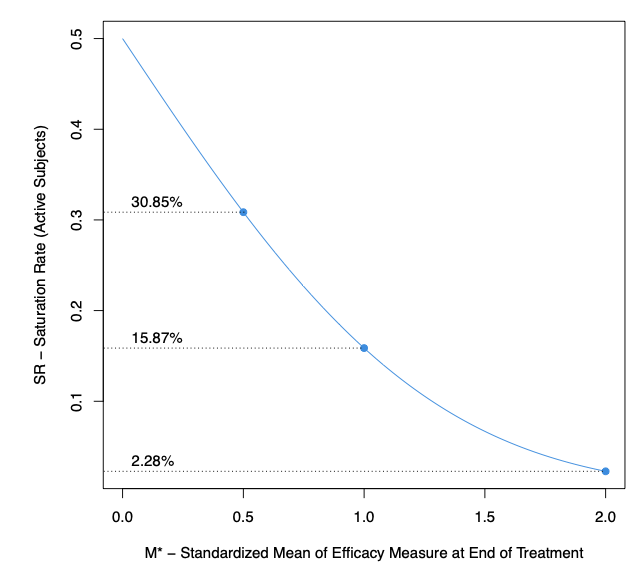
Figure 2: Saturation Rate of Active Subjects in function of M*, the standardized mean, the ratio between the mean and the standard deviation of the efficacy assessment measured at end of treatment in the active group.
Table 1 presents the impact of a minimum required baseline score as inclusion criterion, on the mitigation of the saturation effect. A case with a high SR without minimum required score (M* = 0.5, N = 100, targeted power = 80%) is considered. With this minimum score going from 0 to 6 (for a measurement ranging from 0 to 10), the saturation drops from 30.51% to 7.35% and the effective power increases from 70.71% to 78.64%.
Table 1: Saturation and Power for different inclusion criteria for a study designed to have a power of 80%, considering a standardized mean of the efficacy measurement at end of treatment equal to 0.5, and a sample size of 100.

Conclusion
Saturation is inherent to the use of finite scales to assess outcomes computed as change from baseline. As it reduces the estimation of treatment effect, it is important to assess how it reduces the chances to observe significant effects in RCT.
In a situation where the efficacy measurement at end of treatment has low mean and high variability, the proportion of saturating subjects is high. This induces an important loss of study power. This drop is even larger if most of the variability at the end of the treatment comes from differences between subjects at baseline rather than from treatment response. Fortunately, using a more restrictive inclusion criterion on the minimum required baseline score is a good solution to reduce this power loss. It reduces the saturation and decreases its impact on the power.
Nevertheless, even with an optimal inclusion criterion, there remains a small proportion of subjects with a saturated outcome. Up to 10% of additional completers might be considered when designing the sample size to ensure the targeted power. Another method to reach the targeted power could be to adjust for prognostic covariates. If power loss is limited (< 5%), an adjustment for covariates explaining 15% of the variance of the outcomes should be sufficient.
Finally, this analysis shows the devastating impacts resulting from saturation. It emphasizes the importance of inclusion criteria commonly used, as well as the the need to quantify the saturation and its impact during the study design phase to reduce the chance of a non-conclusive trial.

